关于OO_hw_11中qlm指令的一些想法
21373405 周靖宇
Dijkstra
Dijkstra算法是一种常见的求最短路径的算法,网上有很多的板子,就不多说了,记得存下每个最优路径所经过的点。
关于环
我在这里给出三个我自己的定义:
-
第零类环:含起始点的三元或更多元环
-
第一类环:至少存在三个不同的包含起始点在内的节点,记起始点为$v_0$,其结构为$v_0…v_1ev_2…v_0$其中,边$v_0…v_1$和$v_0…v_2$都是最短路径且不存在$v_0$外的重复节点。
-
第二类环:至少存在三个不同的包含起始点在内的节点,记起始点为$v_0$,其结构为$v_0…v_1ev_0$其中,边$v_0…v_1$是最短路径。不难看出,第二类图其实是第一类图的特殊情况。
首先给出结论,包括起始点$v_0$的最小至少三元环的最终形态为第一类环或者第二类环。想找最小遍历即可,要是没有第一类环或者第二类环,则不存在第零类环,下面是证明。注意,下面的最短路径都是迪杰斯特拉算法跑出来的最短路径。
若不存在第一类环也不存在第二类环
首先分析条件,不存在第二类环。
那么对于任意一个点,其到初始点的最短路径就是直连,否则其最短路径至少还包括一个起始点之外的点,其构成了第二类环。因此所有点的最优距离均为直连到初始点,而且任意两个初始点之外的点不相邻,否则构成了第一类环。则显然,这样的图是不可能存在第零类环的。
证明结论的正确性
我们证明,若至少存在一个第零类环,最小第零类环的最终形态为第一类环或者第二类环。
任取一个第零类环,不妨设为$v_0ev_1ev_2…v_nev_0$,我们证明至少存在一个第一类环或者第二类环,其权重之和小于等于此环。
$Path_i$是$v_i$的最优路径
取这些环
$$
Path_iePath_{i+1}
$$
即
$$
v_0e…v_iev_{i+1}…v_0
$$
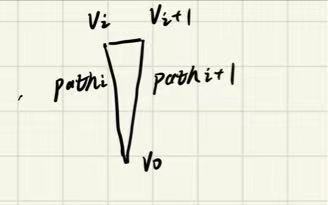
即$v_0…v_i$和$v_0…v_{i+1}$都是最优路径。首先,其权重之和显然小于原本的环。若这些环均不是第一类环,即对于环中任意两个相邻的点,该两点的最优路径总有相交。
$$
\forall i (i > 0 \wedge i < n \wedge (Path[i] - v_0) \cap (Path[i+1] - v_0) \neq \emptyset)
$$
任取两个相邻的点的最优路径,取重合路径中距离$v_0$最近的点$v$,由算法特性知,$v_0…v$为某一个点的最优路径,而因为其距离最近,若其与$v_0$不相邻,存在点$v’$在$v_0…v$的路径上,而由于$v$是距离最短的一个,因此则显然,$v’$不存在,$v$与$v_0$相邻,因此可以得到对于Path[i](i >= 1 && i <= n),其第一步都是一样的。(类似于最小生成树)
取环
$$
Path[n] e v_0ev_n
$$
$$
Path[1] e v_0ev_1
$$
即
$$
v_1ev_0…v_1
$$
$$
v_nev_0…v_n
$$
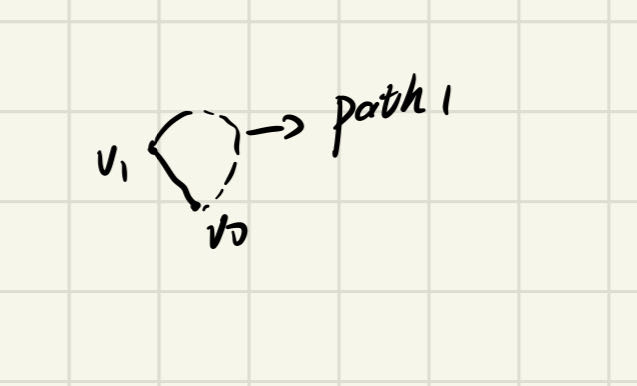
其中$v_0…v_1$和$v_0…v_n$是最优路径,如果其路径上有大于等于三个点,则他为一个第二类环。同上
下证此时这两个图至少有一个为第二类环
若两图均不为第二类图。则两图中至多两个点,因此$v_1$和$v_n$的最佳路径都是直连,由上面的对于任意Path[i]第一步都一样得,Path[1] == Path[n],$v_1v_n$为同一个点,因此环上只有两个点,这与其为一个第零类环矛盾!
因此这两个中至少有一个为第二类环。
因此对于任意的第零类环,都至少有一个第一类或者第二类环,其权重之和小于等于他。取等条件为当其为第一类或第二类环时。因此权重和最小的第零类环为第一类或者第二类环。
因此我们可以通过遍历第一类第二类环来获取最小的权重和。
而大概使用这样的代码遍历就可以找到对应的距离
int ans = INF;
for (int i = 0; i < size; i++) {
if (i == index) {
continue;
}
MyPerson person1 = personArrayList.get(i);
for (int j = 0; j < i; j++) {
MyPerson person2 = personArrayList.get(j);
res.clear();
res.addAll(set[i]);
res.retainAll(set[j]);
if (person1.isLinked(person2) && dist[i] + dist[j] + person1.queryValue(person2) < ans && res.size() == 1 && set[i].size() + set[j].size() >= 4) {
ans = dist[i] + dist[j] + person1.queryValue(person2);
}
}
}
